Taylor Dispersion Analysis (TDA) in DSBC group
The essential of TDA, within a 5-min videoclip:
Principle of TDA
Taylor Dispersion Analysis (TDA) is an absolute and straightforward method for determining diffusion coefficient and thus, hydrodynamic radius. This method is based on the seminal work of Taylor[1] and Aris[2], describing the dispersion of a solute plug in an open tube under Poiseuille laminar flow. The dispersion is due to the combination of the dispersive parabolic velocity profile with the molecular diffusion that redistributes the molecules in cross section of the capillary.

Doing TDA is doing bad chromatography: all the solutes elute in the dead volume time, with no retention. Chromatographically speaking, there is no separation, only dispersion. TDA is a dispersion-based separation technique. Larger species diffuse slowly and are more prone to dispersion due to slow averaging of the velocity profile, leading to broader elution peak. Smaller species diffuse faster, leading to slow dispersion.

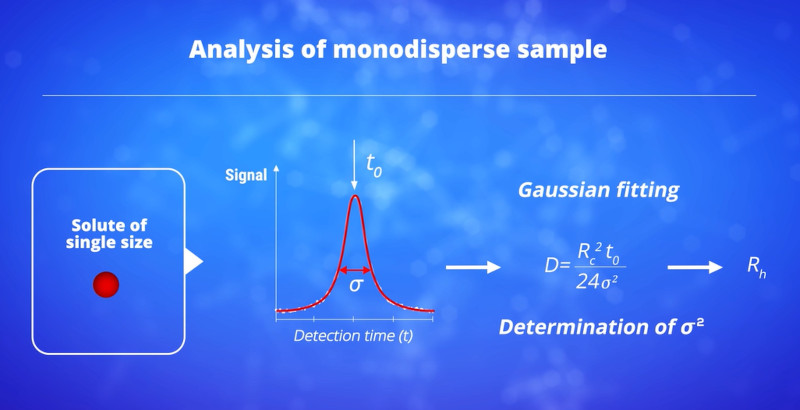
The information about size distribution of the sample is in the dispersion of the elution profile. The broader the peak is, the larger the size of the solute is. For a monodisperse sample, the elution profile is a Gaussian peak. For a polydisperse sample, the elution profile is the sum of different Gaussian contributions. The polydispersity of the sample is in the discrepancy of the elution profile to the Gaussian shape. If you want to know more about TDA principle, you can watch this short video (6’20”)
When axial diffusion is negligible compared to Taylor dispersion, the molecular diffusion coefficient, D, is related to the temporal variance of an analyte, σt2, the average elution time t0 and the capillary radius, Rc, of the tube by the following equation[3]:
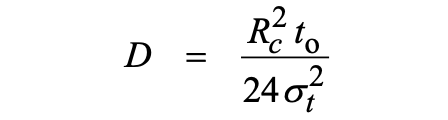 |
(1) |
Knowing the capillary radius, this simple equation allows the absolute determination of the solute diffusion coefficient from the experimental values of the temporal variance and the average elution time t0. The validity of equation (1) is conditioned to the assessment of two requirements. A first condition is that the axial (longitudinal) diffusion is negligible compared to the dispersion due to the parabolic velocity profile. In a recent work, we demonstrated that this first condition could be expressed as a function of the relative error ε on the determination of D that can be tolerated by:[P13]
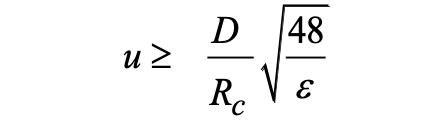 |
(2) |
Taking ε = 3% in in equation (2) leads to:
 |
(3) |
 |
(4) |
If one takes ε = 3%, inequality (4) becomes:
 |
(5) |
Advantages of TDA
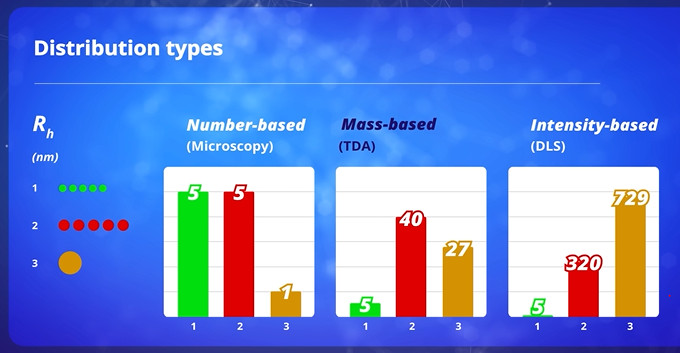
Advantages of Taylor Dispersion Analysis (TDA) include the absence of calibration for the size determination, the insensitivity of the method to the presence of dusts (no need to filtrate the sample), the injection of very small sample volume (few nL), a large size range (between 0.1 and 300 nm), the absence of bias toward larger species, and fast analysis. For a mass-sensitive detector, TDA provides the mass-based size distribution of the sample[P1], which is very different from the number-based distribution obtained by microscopy, or the intensity-based distribution obtained by dynamic light scattering (DLS).
The CRLI approach
In the case of polydisperse sample, the taylorgram is a sum of a different Gaussian peaks corresponding to the different populations of different size constituting the sample. In 2015, we have published[P18] and patented[B1] the use of Constrained Regularized Linear Inversion approach as a new data processing method to extract the probability density functions of the diffusion coefficient (or hydrodynamic radius) from experimental taylorgrams. This approach can be applied to arbitrary polydisperse samples, and gives access to the whole diffusion coefficient distributions, thereby significantly enhancing the potentiality of Taylor dispersion analysis.

Applications of TDA
Due to the high number of applications, it is not possible to cite all of them. A lot of them are still to be discovered. One can cite the size-characterization of proteins[P40], or vaccine antigens[P32,P41], mRNA lipid nanoparticles (LNP) [P35,P38], the monitoring of Aβ peptide aggregation[P33,P36,P39], biopolymer degradation[P21], extracellular vesicles[P42], ultra-high molar mass polyelectrolyte[P37], SEDDS[P22,P25,P27,P31], cubosomes[P24], drug delivery systems[P12,P16] and nanoparticles[P20,P34], polysaccharides[P23,P27], polyplexes[P8,P19,P28], dendrimers [P1,P7,P11] and polymers[P2,P3,P5,P6]. Recent examples of application of TDA to the characterization of mRNA lipid nanoparticle (LNP) is presented in the following short video (2’18”):
History and developments of TDA in the DSBC group
Want to know more about TDA? How did this technique emerge, how was it developed in our research team in collaboration with other researchers (Luca Cipelletti, L2C Montpellier, and Michel Martin, ESPCI Paris) ? Watch this video (13’37”):
References
[1] G. Taylor, Proc. Roy. Soc. Lond. A 1953, 219, 186–203.
[2] R. Aris, Proc. Roy. Soc. Lond. A 1956, 235, 67–77.
(3] A. Alizadeh, C. A. Nieto de Castro, W. A. Wakeham, Int. J. Thermophys. 1980, 1, 243–284.
Patent by DSBC group on TDA:
 B1. Method for determining the size distribution of a mixture of particles using Taylor dispersion and associated systems. H. Cottet, L. Cipelletti, M. Martin, J.-P. Biron, Patent WO2014001409 A1. US20150192507.
B1. Method for determining the size distribution of a mixture of particles using Taylor dispersion and associated systems. H. Cottet, L. Cipelletti, M. Martin, J.-P. Biron, Patent WO2014001409 A1. US20150192507.
Licensed to Nanoscale Metrix (L23038 CNRS).
Complete publication list of DSBC group on TDA:
P42. Fast, simple and calibration-free size characterization and quality control of extracellular vesicles using capillary Taylor dispersion analysis. S. Obeid, J. Chamieh, T. D. Mai, M. Morani, M. Reyre, Z. Krupova, P. Defrenaix, H. Cottet, M. Taverna, J. Chromatogr. A, 2023, 1705, 464189.
P41. Optimization of limit of detection in Taylor dispersion analysis: application to the size determination of vaccine antigens. C. Malburet, M. Martin, L. Leclercq, J.-F. Cotte, J. Thiébaud, J.-P. Biron, J. Chamieh, H. Cottet, Talanta Open, 2023, 7, 100209.
P40. Molecular determinants of fibrillation in a viral amyloidogenic domain from combined biochemical and biophysical studies. J. F. Nilsson, F. Gondelaud, H. Baroudi, G. Pesce, C. Bignon, D. Ptchelkine, J. Chamieh, H. Cottet, A. V. Kajava, S. Longhi, Int. J. Mol. Sci. 2023, 24(1), 399.
P39. Taylor dispersion analysis discloses the impairment of Aβ peptide aggregation by the presence of a fluorescent tag. M. Deleanu, J.-F. Hernandez, H. Cottet, J. Chamieh, Electrophoresis, 2023, 44(7–8), 701–710.
P38. Taylor dispersion analysis to support lipid-nanoparticle formulations for mRNA vaccines. C. Malburet, L. Leclercq, J.-F. Cotte, J. Thiébaud, E. Bazin, M. Garinot, H. Cottet, Gene Ther., 2022, 30(5), 421–428.
P37. Determination of ultrahigh molar mass of polyelectrolytes by Taylor dispersion analysis. X. Leclercq, L. Leclercq, A. Guillard, L. Rodriguez, O. Braun, C. Favero, H. Cottet. J. Chromatogr. A, 2022, 1670, 462949.
P36. Taylor dispersion analysis and atomic force microscopy provide quantitative insight on the aggregation kinetics of Aβ(1-40)/Aβ(1-42) amyloid peptide mixtures. M. Deleanu, O. Deschaume, J.-F. Hernandez, L. Cipelletti, C. Bartic, H. Cottet, J. Chamieh, ACS Chem. Neurosci., 2022, 13(6), 786–795.
P35. Size and charge characterization of lipid nanoparticles for mRNA vaccines. C. Malburet, L. Leclercq, J.-F. Cotte, J. Thiébaud, E. Bazin, M. Garinot, H. Cottet, Anal. Chem., 2022, 94(11), 4677–4685.
P34. Biodegradation of metal-based ultra-small nanoparticles: a combined approached using TDA-ICP-MS and CE-ICP-MS. L. Labied, P. Rocchi, T. Doussineau, J. Randon, O. Tillement, H. Cottet, F. Lux, A. Hagège, Anal. Chim. Acta, 2021, 1185, 339081.
P33. Unraveling the speciation of β-amyloid peptides during the aggregation process by Taylor dispersion analysis. M. Deleanu, J.-F. Hernandez, L. Cipelletti, J.-P. Biron, E. Rossi, M. Taverna, H. Cottet, J. Chamieh, Anal. Chem., 2021, 93, 6523–6533.
P32. Antigen-adjuvant interactions in vaccines by Taylor dispersion analysis: size characterization and binding parameters. C. Malburet, L. Leclercq, J. F. Cotte, J. Thiébaud, S. Marco, M. C. Nicolaï, H. Cottet, Anal. Chem., 2021, 93, 6508–6515.
P31. Co-solvents in self-emulsifying drug delivery systems (SEDDS) – do they really solve our solubility problems? A. M. Jörgensen, J. D. Friedl, R. Wibel, J. Chamieh, H. Cottet, A. Bernkop-Schnürch, Mol. Pharmaceut., 2020, 17(9), 3236–3245.
P30. Mass transfer efficiency in rare earths extraction using a hollow fiber pertraction device. M. Toure, J. Chamieh, G. Arrachart, S. Pellet-Rostaing, H. Cottet, J. Duhamet, Separation and Purification Technology, 2020, 251, 117330.
P29. Size-based characterization of polysaccharides by Taylor dispersion analysis with photochemical oxidation or back scattering interferometry detections. L. Leclercq, P. Saetear, A. Rolland-Sabaté, J.-P. Biron, J. Chamieh, L. Cipelletti, D. J. Bornhop, H. Cottet, Macromolecules, 2019, 52, 4421–4431.
P28. Supramolecular self-assembly of DNA with a cationic polythiophene – From polyplexes to fibers. M. Leclercq, J. Rubio-Magnieto, D. Mohammed, S. Gabriele, L. Leclercq, H. Cottet, S. Richeter, S. Clément, M. Surin, ChemNanoMat, 2019, 5, 703–709.
P27. Peptide release from SEDDS containing hydrophobic ion pair therapeutic peptides measured by Taylor dispersion analysis. J. Chamieh, A. Domènech Tarrat, C. Doudou, V. Jannin, F. Demarne, H. Cottet, Int. J. Pharm., 2019, 559, 228–234.
P26. Size-characterization of natural and synthetic polyisoprenes by Taylor dispersion analysis. J. P. Biron, F. Bonfils, L. Cipelletti, H. Cottet, Polymer Testing. 2018, 66, 244–250.
P25. Size characterization of lipid-based self-emulsifying pharmaceutical excipients during lipolysis using Taylor dispersion analysis with fluorescence detection. J. Chamieh, H. Merdassi, J.-C. Rossi, V. Jannin, F. Demarne, H. Cottet, Int. J. Pharm., 2018, 537, 94–101.
P24. Limits in size of Taylor dispersion analysis: representation of the different hydrodynamic regimes and application to the size-characterization of cubosomes. J. Chamieh, L. Leclercq, M. Martin, S. Slaoui, H. Jensen, J. Østergaard, H. Cottet, Anal. Chem. 2017, 89, 13487–13493.
P23. Taylor dispersion analysis of polysaccharides using backscattering interferometry. P. Saetear, J. Chamieh, M. Kammer, T. J. Manuel, J. P. Biron, D. J. Bornhop, H. Cottet, Anal. Chem., 2017, 89, 6710–6718.
P22. Hydrodynamic size characterization of a self-emulsifying lipid pharmaceutical excipient by Taylor dispersion analysis with fluorescent detection. J. Chamieh, V. Jannin, F. Demarne, H. Cottet, Int. J. Pharm., 2016, 513, 262–269.
P21. Monitoring biopolymer degradation by Taylor dispersion analysis. J. Chamieh, J.-P. Biron, L; Cipelletti, H. Cottet, Biomacromolecules, 2015, 16, 3945–3951.
P20. Size-based characterization of nanoparticle mixtures by the inline coupling of Capillary Electrophoresis to Taylor dispersion analysis. F. Oukacine, A. Morel, I. Desvignes, H. Cottet J. Chromatogr. A. 2015, 1426, 220–225.
P19. Fast characterization of polyplexes by Taylor dispersion analysis. L. Leclercq, S. Reinhard, J. Chamieh, E. Wagner, H. Cottet, Macromolecules, 2015, 48, 7216–7221.
P18. Measuring arbitrary diffusion coefficient distributions of nano-objects by Taylor dispersion analysis. L. Cipelletti, J.-P. Biron, M. Martin, H. Cottet, Anal. Chem., 2015, 87, 8489–8496.
P17. Size characterization of commercial micelles and microemulsions by Taylor dispersion analysis. J. Chamieh, F. Davanier, V. Jannin, F. Demarne, H. Cottet, Int. J. Pharm., 2015, 492, 46–54.
P16. Physico-chemical characterization of polymeric micelles loaded with platinum derivatives by capillary electrophoresis and related methods. F. Oukacine, S. Bernard, I. Bobe, H. Cottet, J. Control. Release, 2014, 196, 139–145.
P15. Investigating the influence of phosphate ions on poly-L-lysine conformations by Taylor dispersion analysis. X. Jin, L. Leclercq, N. Sisavath, H. Cottet, Macromolecules, 2014, 47, 5320–5327.
P14. Polydispersity analysis of Taylor dispersion data: the cumulant method. L. Cipelletti, J.-P. Biron, M. Martin, H. Cottet, Anal. Chem., 2014, 86, 6471–6478.
P13. On the optimization of operating conditions for Taylor dispersion analysis of Mixtures. H. Cottet, J. P. Biron, M. Martin, Analyst, 2014, 139, 3552–3562.
P12. Size and charge characterization of polymeric drug delivery systems by Taylor dispersion analysis and capillary electrophoresis. A. Ibrahim, R. Meyrueix, G. Pouliquen, Y. P. Chan, H. Cottet, Anal. Bioanal. Chem., 2013, 405(16), 5369–5379.
P11. Monitoring surface functionalization of dendrigraft poly-L-lysines via click chemistry by capillary electrophoresis and Taylor dispersion Analysis. T. Liu, F. Oukacine, H. Collet, A. Commeyras, L. Vial, H. Cottet. J. Chromatogr. A, 2013, 1273, 111–116.
P10. Comparison of single and double detection points Taylor dispersion analysis for monodisperse and polydisperse samples. J. Chamieh, H. Cottet, J. Chromatogr. A., 2012, 1241, 123–127.
P9. Taylor dispersion analysis with two detection points on a commercial capillary electrophoresis apparatus. J. Chamieh, F. Oukacine, H. Cottet, J. Chromatogr. A., 2012, 1235, 174–177.
P8. Fast characterization of polyelectrolyte complexes by the inline coupling of capillary electrophoresis to Taylor dispersion analysis. L. Leclercq, H. Cottet, Anal. Chem., 2012, 84, 1740–1743.
P7. Hydrodynamic behavior of dendrigraft polylysines in water and dimethylformamide. N. Yevlampieva, A. Dobrodumov, O. Nazarova, O. Okatova, H. Cottet, Polymers, 2012, 4, 20–31.
P6. Determination of individual diffusion coefficients in evolutive binary mixtures by Taylor dispersion analysis: application to the monitoring of polymer reaction. H. Cottet, J.-P. Biron, L. Cipelletti, R. Matmour, M. Martin. Anal. Chem. 2010, 82, 1793–1802.
P5. Size-based characterization of an ionic polydiacetylene by Taylor dispersion analysis and capillary electrophoresis. J. Deschamps, S. G. Dutremez, B. Boury, H. Cottet, Macromolecules, 2009, 42, 2679–2685.
P4. Non uniform surface charge distributions in capillary electrophoresis: theoretical and experimental approach based on Taylor dispersion. G. Danger, R. Pascal, H. Cottet. Electrophoresis, 2008, 29, 4226–4237.
P3. Size-based characterization by the coupling of Capillary Electrophoresis to Taylor dispersion analysis. T. Le Saux, H. Cottet. Anal. Chem., 2008, 80, 1829–1832.
P2. Taylor dispersion analysis of mixtures. H. Cottet, J.-P. Biron, M. Martin, Anal. Chem., 2007, 79, 9066–9073.
P1. Determination of dendrigraft poly-L-lysine diffusion coefficients by Taylor dispersion analysis. H. Cottet, M. Martin, A. Papillaud, E. Souaid, H. Collet, A. Commeyras, Biomacromolecules, 2007, 8, 3235–3243.



